用 Tarjan 算法求解无向图的割点和割边

上期回顾：https://www.cnblogs.com/ofnoname/p/18823922
Tarjan 算法与无向图

连接性分析是图论的核心，而Tarjan算法为我们提供了穿透复杂网络结构的通用方法。之前，我们深入探讨了Tarjan如何利用深度优先搜索(DFS) 的时间戳(dfn[])和回溯值(low[]) 的概念，高效地识别有向图中的强连通分量(SCC)。这种方法通过维护栈结构和巧妙的时间戳比较，将看似复杂的连通性问题转化为优雅的线性时间解决方案。
现在，当我们从有向图转向无向图领域，一个全新的连通性问题浮出水面：如何识别无向图中的割点(cut vertices) 和割桥(bridges)？
有趣的是，尽管问题领域不同，Tarjan算法展现出了惊人的通用性。在无向图中，DFS遍历同样会生成一棵搜索树，但这里有一个关键差异：由于无向图任两点总是互相可达（连通的话），无向图的DFS树不存在横叉边。当我们在无向图上执行DFS时，所有非树边都必然是连接节点与其祖先的返祖边(back edges)。这一特性简化了连通性分析，使得我们可以继续延用dfn和low这对黄金搭档：

• dfn：节点u的DFS访问时间戳（不变的含义）
  
• low：记录节点u通过树边和最多一条返祖边能到达的最小时间戳
  

理解无向图割点不仅具有理论价值，更是许多实际系统的基石。想象一下：当这些关键节点代表网络路由器、电力枢纽或社交网络中的信息桥梁时，识别它们就成为了系统可靠性的第一道防线。这也是网络可靠性分析、社交网络关键人物识别、交通枢纽规划等实际应用中的核心问题。
无向图割点问题

在无向图 \(G=(V,E)\) 中，顶点 u 被称为割点(cut vertex/articulation point)，当且仅当删除 u 及其关联边后，图的连通分量数量增加。
想象一个现实的网络：割点就像关键枢纽站，如果它瘫痪，整个网络会被分割成孤立区域；社交网络中，割点就是那个连接不同社群的关键人物；在计算机网络中，割点相当于核心路由器，一旦故障会导致子网断开连接。

割点的求解

总不可能依次去掉点来验证新图是否连通吧！这是仍需要使用 Tarjan 算法。

• 初始化：
  
  
  
  • 为每个节点维护两个数组：dfn为DFS访问 u 的时间戳；low为 u 通过树边或一条返祖边能到达的最小时间戳
    
  • 设置全局计数器timestamp，统计时间戳
    
  
  
• DFS遍历：进行遍历，按照规则更新时间戳和可达的最小时间戳数组。
  

1. def dfs(u, parent):
2.    初始化 dfn[u] = low[u]
3.    child_count = 0
5.    for v in neighbors(u):
6.        if v == parent: continue  # 关键：跳过父节点
8.        if not visited[v]:
9.            child_count += 1
10.            dfs(v, u)
11.            low[u] = min(low[u], low[v])  # 更新回溯值
13.            # 割点判断条件
14.            if (u不是根 and low[v] >= dfn[u]) or
15.               (u是根 and child_count >= 2):
16.                mark u as cut vertex
17.        else:
18.            low[u] = min(low[u], dfn[v])  # 处理返祖边

复制代码

• 割点判断条件：
  
  
  
  • 根节点：当且仅当在DFS树中有≥2个子树
    
  • 非根节点：当且仅当存在子节点v满足low[v] >= dfn
    
  
  

正确性证明

为什么low[v] >= dfn能检测割点？
按照定义，low[v] >= dfn意味着v的子树无法绕过u访问更早的祖先，删除u后，v的子树将与其他部分断开。反证：若存在其他路径，则low[v]应小于dfn

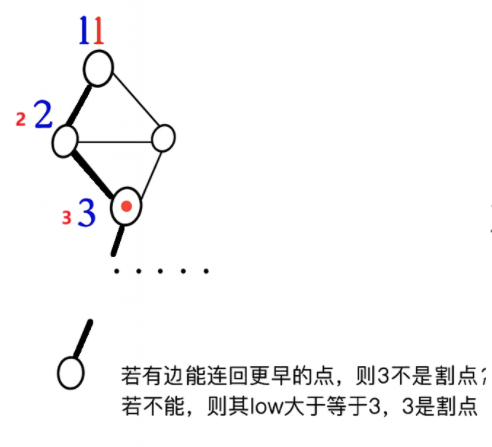
而根节点比较特殊，因为其在搜索树中没有父节点了。只要他有大于1个子树，删除根节点就会让子树分开，所以根节点是割点。
[code]class Graph {    vector edges;  // 邻接表    int n;                     // 顶点数    int time = 0;              // 全局时间戳    vector disc;          // 发现时间(dfn)    vector low;           // 回溯值    vector isCut;        // 记录割点    vector parent;        // 父节点数组    void dfs(int u) {        disc = low = ++time;        int children = 0;  // 记录子树数量                for (int v : edges) {            // 跳过父节点            if (v == parent) continue;                        if (disc[v] == 0) {  // 未访问                parent[v] = u;                children++;                dfs(v);                                // 更新当前节点的low值                low = min(low, low[v]);                                // 非根节点割点判断                if (parent != -1 && low[v] >= disc) {                    isCut = true;                }            }             // 处理返祖边            else {                low = min(low, disc[v]);            }        }                // 根节点特殊判断        if (parent == -1 && children >= 2) {            isCut = true;        }    }public:    Graph(int n) : n(n), edges(n), disc(n, 0), low(n, 0),                   isCut(n, false), parent(n, -1) {}        // 无向图添加双向边    void addEdge(int u, int v) {        edges.push_back(v);        edges[v].push_back(u);    }        // 寻找所有割点    vector findCutVertices() {        for (int i = 0; i < n; ++i) {            if (disc == 0) {                parent = -1;  // 标记为根                dfs(i);            }        }                vector result;        for (int i = 0; i < n; ++i) {            if (isCut) result.push_back(i);        }        return result;    }        void printCutVertices() const {        cout  dfn 意味着v的子树甚至无法到达u本身</ul>

几何解释：
设 u 是 v 的父节点，边 (u,v) 为树边：

• 若存在返祖边使low[v] = dfn，则v的子树能直接连回u
  
• 若low[v] > dfn，则v的子树只能到达比u更晚的节点
  
• 删除 (u,v) 后，v 的子树与 u 的连通性被完全破坏
  

[code]class Graph {    // ...    vector bridges;  // 新增：存储割边    void dfs(int u) {        // ...            if (disc[v] == 0) {  // 未访问节点                // ...                // 割边判断（关键修改：> 而非 >=）                if (low[v] > disc) {                    bridges.push_back({min(u, v), max(u, v)});  // 避免重复                }            }             else {  // 已访问节点（返祖边）                low = min(low, disc[v]);            }        }                // 根节点割点判断        if (parent == -1 && children >= 2) {            isCut = true;        }    }public:    Graph(int n) : n(n), edges(n), disc(n, 0), low(n, 0),                   parent(n, -1), isCut(n, false) {}        void addEdge(int u, int v) {        edges.push_back(v);        edges[v].push_back(u);    }        // 返回割点列表    vector getCutVertices() {        // 初始化        fill(disc.begin(), disc.end(), 0);        fill(low.begin(), low.end(), 0);        fill(parent.begin(), parent.end(), -1);        fill(isCut.begin(), isCut.end(), false);        bridges.clear();        time = 0;                for (int i = 0; i < n; ++i) {            if (disc == 0) dfs(i);        }                vector result;        for (int i = 0; i < n; ++i) {            if (isCut) result.push_back(i);        }        return result;    }        // 返回割边列表（按字典序排序）    vector getBridges() {        getCutVertices();  // 计算同时获取割点和割边        sort(bridges.begin(), bridges.end());  // 排序保证输出一致        return bridges;    }        void printBridges() {        auto res = getBridges();        cout