模拟退火算法的原理与实现示例

  模拟退火算法（Simulated Annealing, SA）是一种受物理中固体退火过程启发的元启发式优化算法，用于在大规模搜索空间中寻找近似全局最优解。其核心思想是通过模拟物理退火过程中的“温度”下降和粒子热运动，逐步收敛到低能量（即目标函数更优）的状态。
一、基本原理

1. 物理退火类比

  在固体退火中，材料被加热至高温后缓慢冷却，原子从高能态逐渐趋于有序排列，最终达到能量最低的稳定状态。模拟退火算法将这一过程抽象为：
  温度（T）：控制搜索的随机性。
  能量（E）：对应目标函数值（需最小化的代价或最大化的问题的适应度）。
2. Metropolis准则

  算法以一定概率接受比当前解更差的解，避免陷入局部最优。
  对于新解\(x_{new}\)和当前解\(x_{current}\)：
    若\(\Delta E=E(x_{mew})-E(x_{current})\leq 0 \quad (更优解)\)，直接接受。
    若\(\Delta E > 0 \quad (更差解)\)，以概率\(P=e^{-\Delta E/T}\)接受。
3. 温度调度（Cooling Schedule）

  初始高温时，算法广泛探索解空间；随着温度降低，逐渐倾向于局部优化。
  温度下降方式：如指数下降\(T_{k+1}=\alpha T_k \quad (\alpha\in(0,1)为冷却系数)\)。
二、算法步骤

1. 初始化

  随机生成初始解\(x_0\)。
  设置初始温度\(T_0\) 、终止温度\(T_{min}\)、冷却系数\(\alpha\)。
2. 迭代过程

  生成新解：在当前解附近随机扰动（如交换、位移等操作）产生候选解\(x_{new}\)。
  评估解：计算目标函数差值\(\Delta E\)。
  接受准则：根据Metropolis准则决定是否接受\(x_{new}\)。
  降温：更新温度\(T=\alpha T\)。
  终止条件：温度降至\(T_{min}\) 或达到最大迭代次数。
三、参数选择

  初始温度：足够高以使初始接受概率接近1（如\(P_{initial}\approx 0.8\)）。
  冷却系数：典型值\(\alpha \in [0.85,0.99]\)。
  终止条件：温度趋近于0或解长时间无改进。
四、算法特点及优缺点

算法特点

  逃离局部最优：通过概率性接受劣解，增强全局搜索能力。
  收敛性：在足够慢的降温速度下，理论上能以概率1收敛到全局最优解（但实际中难以实现）。
  灵活性：适用于连续或离散优化问题，只需定义解表示、邻域结构和目标函数。
优缺点

  优点：简单通用，适合非线性、多峰问题。
  缺点：收敛速度慢，参数调优依赖经验。
五、应用场景

  组合优化（如旅行商问题TSP、调度问题）。
  函数优化（连续/非凸函数）。
  机器学习（参数调优、神经网络训练）。
六、Python实现示例

1. import matplotlib
2. matplotlib.use('TkAgg')
4. import numpy as np
5. import matplotlib.pyplot as plt
7. plt.rcParams['font.sans-serif'] = ['SimHei']  # 中文支持
8. plt.rcParams['axes.unicode_minus'] = False  # 负号显示
10. # 目标函数：Rastrigin函数，常用于优化算法测试
11. def objective_function(x):
12.     A = 10  # Rastrigin函数参数
13.     n = len(x)  # 问题维度
14.     return A * n + sum([(xi ** 2 - A * np.cos(2 * np.pi * xi)) for xi in x])
17. # 模拟退火算法实现
18. def simulated_annealing(initial_state, objective_function, initial_temperature=100, cooling_rate=0.95,
19.                         num_iterations=1000, perturbation_scale=0.1):
20.     # 初始化当前状态和最优状态
21.     current_state = initial_state.copy()
22.     best_state = initial_state.copy()
23.     current_energy = objective_function(current_state)
24.     best_energy = current_energy
26.     # 记录迭代过程
27.     energies = [current_energy]
28.     temperatures = [initial_temperature]
29.     states = [current_state.copy()]
31.     temperature = initial_temperature
33.     for iteration in range(num_iterations):
34.         # 生成邻域解（扰动当前解）
35.         neighbor = current_state + np.random.normal(0, perturbation_scale, len(current_state))
37.         # 计算新解的能量
38.         neighbor_energy = objective_function(neighbor)
40.         # 计算能量差
41.         delta_energy = neighbor_energy - current_energy
43.         # 判断是否接受新解
44.         if delta_energy < 0 or np.random.rand() < np.exp(-delta_energy / temperature):
45.             current_state = neighbor
46.             current_energy = neighbor_energy
48.             # 更新最优解
49.             if current_energy < best_energy:
50.                 best_state = current_state.copy()
51.                 best_energy = current_energy
53.         # 降温
54.         temperature *= cooling_rate
56.         # 记录当前迭代结果
57.         energies.append(current_energy)
58.         temperatures.append(temperature)
59.         states.append(current_state.copy())
61.         # 打印进度
62.         if (iteration + 1) % 100 == 0:
63.             print(f"Iteration {iteration + 1}/{num_iterations}, "
64.                   f"Current Energy: {current_energy:.4f}, "
65.                   f"Best Energy: {best_energy:.4f}, "
66.                   f"Temperature: {temperature:.4f}")
68.     return {
69.         'best_state': best_state,
70.         'best_energy': best_energy,
71.         'energies': np.array(energies),
72.         'temperatures': np.array(temperatures),
73.         'states': np.array(states)
74.     }
77. # 运行模拟退火算法
78. np.random.seed(42)  # 设置随机种子以便结果可重现
79. initial_state = np.random.uniform(-5.12, 5.12, 2)  # 二维Rastrigin函数的初始解
80. result = simulated_annealing(
81.     initial_state,
82.     objective_function,
83.     initial_temperature=100,
84.     cooling_rate=0.99,
85.     num_iterations=2000,
86.     perturbation_scale=0.5
87. )
89. # 打印结果
90. print("\n优化结果:")
91. print(f"最优解: {result['best_state']}")
92. print(f"最优值: {result['best_energy']:.4f}")
94. # 可视化优化过程
95. plt.figure(figsize=(15, 5))
97. # 绘制能量变化曲线
98. plt.subplot(1, 2, 1)
99. plt.plot(result['energies'])
100. plt.title('能量变化')
101. plt.xlabel('迭代次数')
102. plt.ylabel('能量值')
103. plt.grid(True)
105. # 绘制温度变化曲线
106. plt.subplot(1, 2, 2)
107. plt.plot(result['temperatures'])
108. plt.title('温度变化')
109. plt.xlabel('迭代次数')
110. plt.ylabel('温度')
111. plt.grid(True)
113. plt.tight_layout()
114. plt.show()

复制代码

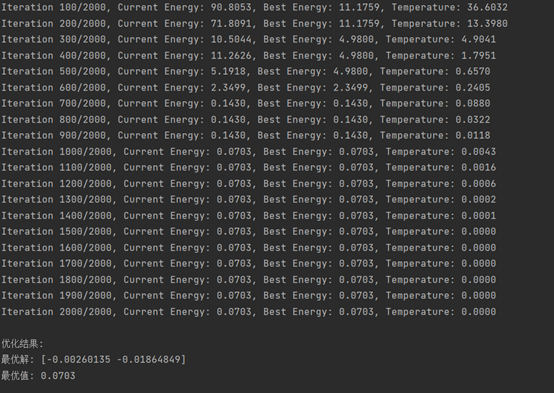
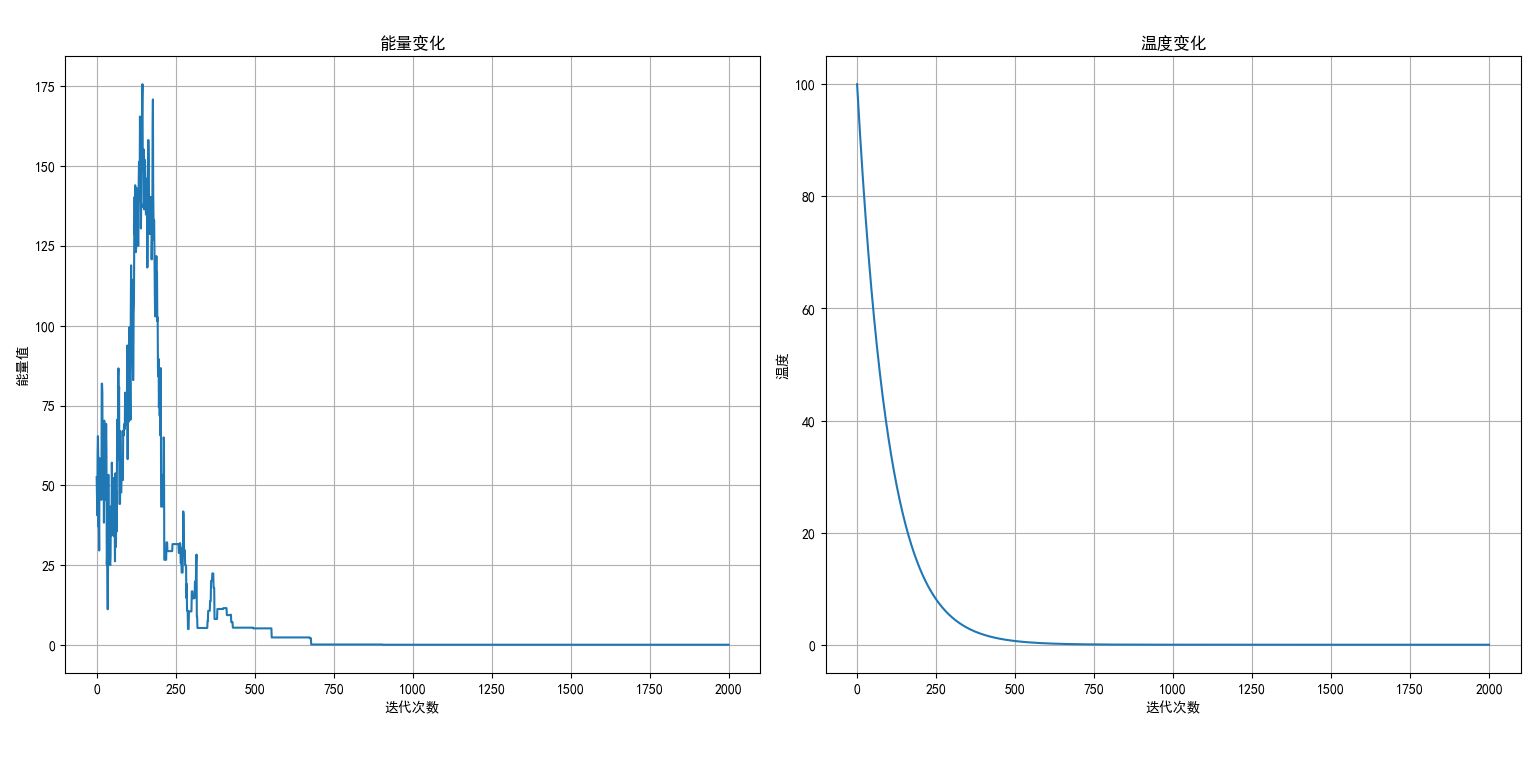
  示例实现了模拟退火算法来求解 Rastrigin 函数的最小值。代码包含以下部分：
  目标函数：定义了 Rastrigin 函数作为优化目标
  算法实现：完整的模拟退火算法，包括解的扰动、接受准则和温度更新
  可视化：展示优化过程中能量和温度的变化趋势
  主要参数包括初始温度、降温速率、迭代次数和扰动规模，可根据需要调整这些参数来优化搜索效果。
七、小结

  模拟退火算法通过 “高温探索、低温收敛” 的策略，平衡了随机性（跳出局部最优）和确定性（向全局最优收敛），是一种高效的全局优化方法。

来源：豆瓜网用户自行投稿发布，如果侵权，请联系站长删除