粒子群算法的原理与实现示例

  粒子群算法（Particle Swarm Optimization，PSO）是一种基于群体智能的优化算法，由 Kennedy 和 Eberhart 于 1995 年提出，其灵感来源于鸟群觅食、鱼群游动等自然界中群体行为的协作与信息共享机制。该算法通过模拟群体中个体（粒子）的运动和信息交互，在解空间中搜索最优解，具有实现简单、收敛速度快、参数少等特点，被广泛应用于函数优化、神经网络训练、工程设计等领域。
一、算法思想

  PSO通过模拟群体中个体（粒子）的协作与信息共享来寻找最优解。每个粒子代表解空间中的一个候选解，通过跟踪自身和群体的历史最优信息，不断调整自身位置（解），来逼近全局最优解。
二、基本概念

  粒子（Particle）：每个粒子有位置（Position）和速度（Velocity）两个属性，位置对应解空间中的一个点，速度决定粒子下一步的移动方向和距离。
  适应值（Fitness）：根据目标函数计算的值，用于评价粒子的优劣。
  个体最优（pBest）：粒子自身历史上找到的最佳位置。
  全局最优（gBest）：整个群体中所有粒子找到的最佳位置（或局部邻域最优，如拓扑结构的变体）。
三、算法流程

1. 初始化

  a) 随机生成一群粒子，初始化其位置和速度。
  b) 计算每个粒子的适应值，记录个体最优（pBest）和全局最优（gBest）。
2. 迭代更新

  每次迭代中，粒子通过以下公式更新速度和位置：

\[v_i^{t+1}=w\cdot v_i^t+c_1\cdot r_1\cdot (pBest_i-x_i^t)+c_2\cdot r_2(gBest-x_i^t)\]

\[x_i^{t+1}=x_i^t+v_i^{t+1}\]
其中，
  \(v_i^t\)：粒子\(i\)在时刻\(t\)的速度。
  \(x_i^t\)：粒子\(i\)在时刻\(t\)的位置。
  \(w\)：惯性权重，平衡全局探索与局部开发。
  \(c_1,c_2\)：学习因子（通常设为2），分别控制个体和群体经验的影响。
  \(r_1,r_2\)：[0,1]内的随机数，增加随机性。
3. 更新最优值

  计算新位置的适应值，更新pBest和gBest。
4. 终止条件

  算法通过多次迭代优化，直到满足以下任一条件时停止：
  a) 达到预设的最大迭代次数；
  b) 全局最优解的精度满足问题要求（如与目标值的误差小于阈值）；
  c) 全局最优解在连续多轮迭代中不再变化（收敛稳定）。
四、关键参数

1. 惯性权重\(w\)

  较大的\(w\)（如0.9）增强全局搜索能力（适合探索新区域），较小的\(w\)（如0.4）增强局部搜索能力（适合精细优化）。实际应用中常采用线性递减策略（如从 0.9 降至 0.4），兼顾前期探索和后期收敛。
2. 学习因子\(c_1,c_2\)

  \(c_1\)反映粒子的 “个体认知”能力，\(c_2\)反映“社会协作”能力。两者平衡决定了粒子是倾向于自身经验还是群体信息。
3. 粒子群规模

  规模过小可能导致搜索不充分，规模过大会增加计算量，通常取 20~100。
五、优缺点

  优点：实现简单，无需梯度信息（适用于非连续、非可微函数），收敛速度快，鲁棒性强。
  缺点：易陷入局部最优解（尤其在高维复杂问题中），对参数设置较敏感，后期收敛速度可能变慢。
六、Python示例

1. import matplotlib
2. matplotlib.use('TkAgg')
4. import numpy as np
5. import matplotlib.pyplot as plt
7. plt.rcParams['font.sans-serif'] = ['SimHei']  # 中文支持
8. plt.rcParams['axes.unicode_minus'] = False  # 负号显示
10. # 定义目标函数（这里使用Rastrigin函数）
11. def rastrigin(x, A=10):
12.     return A * len(x) + sum([(xi ** 2 - A * np.cos(2 * np.pi * xi)) for xi in x])
15. # 粒子群算法实现
16. def particle_swarm_optimization(objective_func, dim, num_particles, max_iter,
17.                                 x_min, x_max, w=0.7, c1=1.5, c2=1.5):
18.     # 初始化粒子位置和速度
19.     particles_position = np.random.uniform(x_min, x_max, size=(num_particles, dim))
20.     particles_velocity = np.random.uniform(-1, 1, size=(num_particles, dim))
22.     # 初始化个体最优位置和全局最优位置
23.     particles_best_position = particles_position.copy()
24.     particles_best_value = np.array([objective_func(p) for p in particles_position])
25.     global_best_index = np.argmin(particles_best_value)
26.     global_best_position = particles_best_position[global_best_index].copy()
27.     global_best_value = particles_best_value[global_best_index]
29.     # 迭代优化
30.     history = []
31.     for iteration in range(max_iter):
32.         for i in range(num_particles):
33.             # 更新速度和位置
34.             r1, r2 = np.random.rand(2)
35.             particles_velocity[i] = (w * particles_velocity[i] +
36.                                      c1 * r1 * (particles_best_position[i] - particles_position[i]) +
37.                                      c2 * r2 * (global_best_position - particles_position[i]))
38.             particles_position[i] += particles_velocity[i]
40.             # 边界处理
41.             particles_position[i] = np.clip(particles_position[i], x_min, x_max)
43.             # 计算新的适应度值
44.             fitness = objective_func(particles_position[i])
46.             # 更新个体最优
47.             if fitness < particles_best_value[i]:
48.                 particles_best_value[i] = fitness
49.                 particles_best_position[i] = particles_position[i].copy()
51.                 # 更新全局最优
52.                 if fitness < global_best_value:
53.                     global_best_value = fitness
54.                     global_best_position = particles_position[i].copy()
56.         history.append(global_best_value)
57.         if iteration % 10 == 0:
58.             print(f"迭代 {iteration}, 最优值: {global_best_value:.4f}")
60.     return global_best_position, global_best_value, history
63. # 运行粒子群算法
64. dim = 2  # 问题维度
65. num_particles = 30  # 粒子数量
66. max_iter = 100  # 最大迭代次数
67. x_min, x_max = -5.12, 5.12  # 搜索空间范围
69. best_position, best_value, history = particle_swarm_optimization(
70.     rastrigin, dim, num_particles, max_iter, x_min, x_max
71. )
73. print(f"\n优化结果:")
74. print(f"最优位置: {np.round(best_position, 4)}")
75. print(f"最优值: {best_value:.4f}")
77. # 可视化
78. plt.figure(figsize=(12, 5))
80. # 绘制收敛曲线
81. plt.subplot(1, 2, 1)
82. plt.plot(history)
83. plt.title('收敛曲线')
84. plt.xlabel('迭代次数')
85. plt.ylabel('最优值')
86. plt.grid(True)
88. # 绘制目标函数和最终粒子位置
89. if dim == 2:
90.     plt.subplot(1, 2, 2)
91.     x = np.linspace(x_min, x_max, 100)
92.     y = np.linspace(x_min, x_max, 100)
93.     X, Y = np.meshgrid(x, y)
94.     Z = np.zeros_like(X)
95.     for i in range(X.shape[0]):
96.         for j in range(X.shape[1]):
97.             Z[i, j] = rastrigin([X[i, j], Y[i, j]])
99.     contour = plt.contourf(X, Y, Z, 50, cmap='viridis')
100.     plt.colorbar(contour)
101.     plt.scatter(best_position[0], best_position[1], c='red', marker='*', s=200, label='最优解')
102.     plt.title('目标函数等高线图')
103.     plt.xlabel('x')
104.     plt.ylabel('y')
105.     plt.legend()
106.     plt.grid(True)
108. plt.tight_layout()
109. plt.show()

复制代码

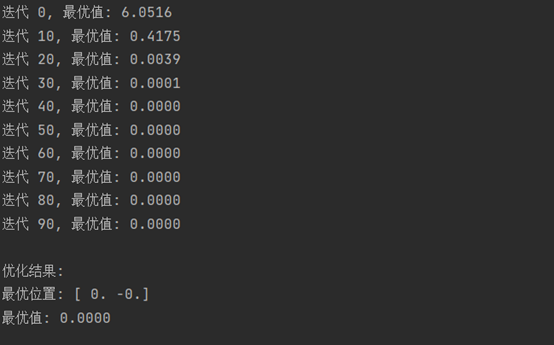
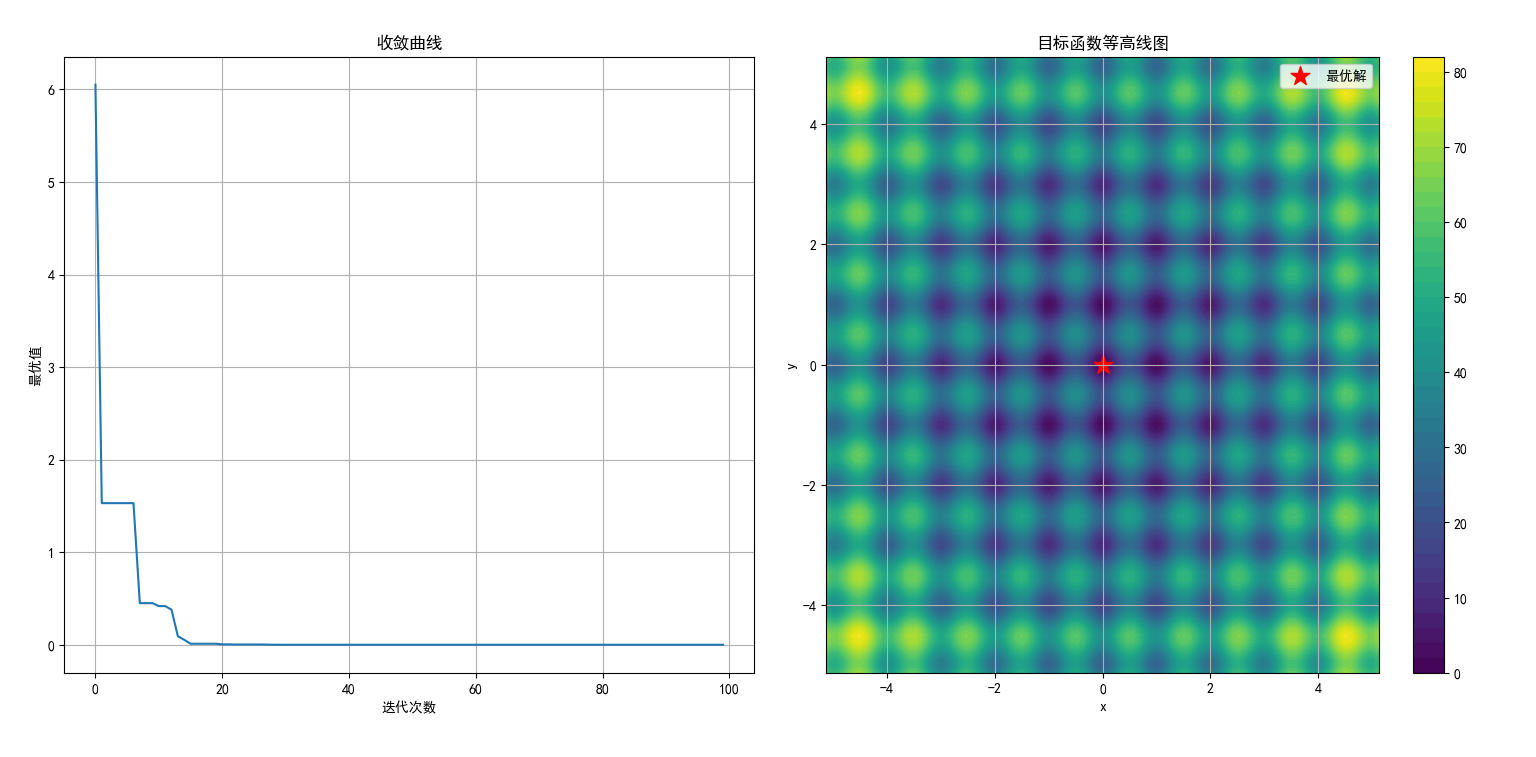
  示例实现了标准的粒子群算法，用于求解 Rastrigin 函数的最小值。包含以下主要部分：
  目标函数定义：使用 Rastrigin 函数作为测试函数，它是一个具有多个局部最小值的复杂函数。
  算法实现：实现了完整的 PSO 算法，包括粒子初始化、速度和位置更新、边界处理等。
  参数设置：可以调整粒子数量、迭代次数、惯性权重和学习因子等参数。
  结果可视化：绘制了算法的收敛曲线和目标函数的等高线图，直观展示优化结果。
七、小结

  粒子群算法通过模拟群体中个体的协作与学习，利用 “个体最优” 和 “全局最优” 引导搜索方向，通过速度和位置的动态更新逐步逼近最优解。其核心是信息共享与群体协作，既保留了个体的探索能力，又通过群体信息加速收敛。在各类优化问题中具有广泛的适用性。

来源：豆瓜网用户自行投稿发布，如果侵权，请联系站长删除